- Joined
- Oct 24, 2003
- Messages
- 11,481
- Reaction score
- 6
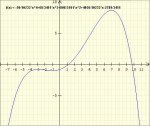
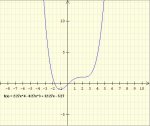
ok, dies ist offensichtlich falsch, da wir für einen Sattelpunkt mindestens eine Funktion mit x^3 benötigen.
ich rechne mal ein paar mögliche schritte vor (ich hoffe ich habe mich nicht verrechnet, aber du kannst es ja mal nachvollziehen
ich rechne mal ein paar mögliche schritte vor (ich hoffe ich habe mich nicht verrechnet, aber du kannst es ja mal nachvollziehen
Code:
a4 - a3 + a2 - a1 + a0 = -1 I
-4a4 + 3a3 - 2a2 + a1 = 0 II
16a4 + 8a3 + 4a2 + 2a1 + a0 = 1 III
32a4 + 13a3 + 8a2 + a1 = 0 IV
48a4 + 12a3 + 2a2 = 0 V
a4 - a3 + a2 - a1 + a0 = -1
-4a4 + 3a3 - 2a2 + a1 = 0
16a4 + 8a3 + 4a2 + 2a1 + a0 = 1 | -I
32a4 + 13a3 + 8a2 + a1 = 0
48a4 + 12a3 + 2a2 = 0
a4 - a3 + a2 - a1 + a0 = -1
-4a4 + 3a3 - 2a2 + a1 = 0
15a4 + 9a3 + 3a2 + 3a1 = 2
32a4 + 13a3 + 8a2 + a1 = 0
48a4 + 12a3 + 2a2 = 0
a4 - a3 + a2 - a1 + a0 = -1 | +II
-4a4 + 3a3 - 2a2 + a1 = 0
15a4 + 9a3 + 3a2 + 3a1 = 2 | -(3*II)
32a4 + 13a3 + 8a2 + a1 = 0 | -II
48a4 + 12a3 + 2a2 = 0
-3a4 + 2a3 - a2 + a0 = -1
-4a4 + 3a3 - 2a2 + a1 = 0
27a4 + 9a2 = 2
36a4 + 10a3 + 10a2 = 0
48a4 + 12a3 + 2a2 = 0




 ):
):