You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
mal wieder mathe -.-
- Thread starter mope7
- Start date
- Joined
- Oct 24, 2003
- Messages
- 11,481
- Reaction score
- 6
Ich habe nichts anderes behauptet, nur muss man natürlich bedenken,das man von der mauer nichts abbrechen kannDas mit der Mauer ist doch eher so gemeint, dass man zu den 100 Metern Zaun zusätzlich 40 Meter für die Umzäunung bekommt, also dass man praktisch 140 Meter Zaun hat, oder?

Was für Aufgaben
70x70 ftw
nanana, dann wäre der Umfang ja 280 ....
du hast ja nur 140 und da wäre es am besten, wenn jede seite 35m lang ist, jedoch ist die mauer ja schon länger, weshalb die andere seite nur 30m lang sein darf.
- Joined
- Jul 28, 2001
- Messages
- 62,725
- Reaction score
- 36
Man muss auch noch ne Tür lassen wo die Autos reinfahren 
Hab den Aufgabentext nicht gelesen
Wieviel kann man denn damit am Tag verdienen James? Wenns mehr als 100 Euro sind dann fahr ich morgen zu Toom und hol Zaun

Hab den Aufgabentext nicht gelesen

Wieviel kann man denn damit am Tag verdienen James? Wenns mehr als 100 Euro sind dann fahr ich morgen zu Toom und hol Zaun

- Joined
- Jul 28, 2001
- Messages
- 62,725
- Reaction score
- 36
Naja dann nähert man sich halt dem Maximum bestmöglich an, die Flächenfunktion wird ja ne Art umgedrehte Parabel sein mit Maximum bei a=b und dem beidseitigen Ende wenn eine Seite Null wird.
Quadratomato
Quadratomato
- Joined
- May 20, 2002
- Messages
- 24,877
- Reaction score
- 5
so, ihr wolltet es so, ihr bekommt es so, die neue Aufgabe *tatatataaaaaa*

--------
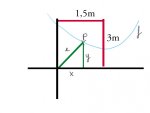
Eine 3m hohe und 1,5m breite Fensterscheibe ist zersprungen. Die Bruchkante lässt sich nach der Ausmessung durch eine parabelförmige Funktion mit der Gleichung f(x) = x² - 3x + 3 beschreiben.
a) Skizzieren Sie den Graphen (habsch, geejay @ me
 )
)b) Berechnen Sie den Punkt P(x|y) des Graphen, der dem Ursprung am nächsten liegt. Wie groß ist dann die minimale Entfernung "e" zum Ursprung ?
c) Um den Schaden zu begrenzen, soll aus dem unteren Reststück eine rechteckige Glasscheibe maximaler Größe herausgeschnitten werden. Welche Abmessungen ergeben sich für die neue Glasscheibe ?
joa, Vorschläge ?

bei b) ist mir als erstes das Näherungsverfahren in den Kopf gesprungen, mal schauen wie ich des mache ^^
Last edited:
- Joined
- May 20, 2002
- Messages
- 24,877
- Reaction score
- 5
x und y = 0 kann ich am Graphen ablesen, das bringt mir nich all zu viel, da die ja auch zimlich weit ausinander liegen

hm, wie wärs mit der ersten Ableitung gegen Null strebend ?
mal checken ^^
edit: hehe, c) is total easy wenn man es zeichnerisch bestimmen darf, dann kann mans auch einfach ablesen

edit2: Näherungsverfahren ist natürlich kappes.
Last edited:
- Joined
- May 20, 2002
- Messages
- 24,877
- Reaction score
- 5
so, hab jetzt mal so angefangen:
1. Extremalbedinung:
e = Wurzel aus x² + y²
2. Nebenbedingung:
y = f(x) = x² - 3x + 3
3. 1 in 2 einsetzen:
e = Wurzel aus x² + (x² - 3x + 3)²
e = Wurzel aus x² + x^4 + 9x² + 9
nur irgendwie hat nen Kamerad da was anderes O_o
edit: Kollege hat folgendes (von der Tafel abgeschrieben, ich war mal wieder nit da
 ): e = Wurzel aus x² - 6x³ + 16x² +9
): e = Wurzel aus x² - 6x³ + 16x² +9wie zum Geier kommt man denn da rauf ? Oo
edit2: ah, binomische Formel, yeah

edit3: zeichnerisch IST es auch (1|1), da haste wahr ^^
Attachments
Last edited:
- Joined
- Oct 24, 2003
- Messages
- 11,481
- Reaction score
- 6
Bei b) würde ich ja blind auf (1|1) Tippen
da müsste man aber zunächst mal prüfen, dass das Delta (der Unterschied) zweier x-Werte die kleiner 1 sind immer kleiner als das Delta der f(x)-Werte ist und umgekehrt, dass das Delta zweier x-Werte die größer 1 sind immer größer als das Delta der f(x)-Werte ist.
Oder anders gesagt, dass der Anstig für x<1 immer kleiner als -1 ist und der Anstieg für x>1 immer größer als -1
c) Solltest du eigentlich aleine schaffen, kannst ja mal sagen, was so deine Gedanken dazu sind
da müsste man aber zunächst mal prüfen, dass das Delta (der Unterschied) zweier x-Werte die kleiner 1 sind immer kleiner als das Delta der f(x)-Werte ist und umgekehrt, dass das Delta zweier x-Werte die größer 1 sind immer größer als das Delta der f(x)-Werte ist.
Oder anders gesagt, dass der Anstig für x<1 immer kleiner als -1 ist und der Anstieg für x>1 immer größer als -1
c) Solltest du eigentlich aleine schaffen, kannst ja mal sagen, was so deine Gedanken dazu sind

- Joined
- May 20, 2002
- Messages
- 24,877
- Reaction score
- 5
sorry, war am telefonieren mit Muddi, hat ein wenig gdauert ^^
also, b hab ich jetzt so halb raus Oo
ausgehend von e = Wurzel aus x^4 - 6x³ + 16x² +9 <-- meine Zielfunktion.
Minimum wenn e²'(x) = 0 , e²''(x) > 0
e²' = 4x3 - 18x^2 + 32x = 0
Nullstelle bei 1 (die anderen beiden Nullstellen sind jetzt mal egal)
e²'' = 12x^2 - 36 x + 32 > 0
x^2 - 3x + 8/3
x1,2 = -3/2 +- Wurzel aus 9/4 -8/3
x1,2 = -3/2 +- Wurzel aus -5/12
--> Error -.- Negative Wurzel geht nit und wenn ichs weglasse bin ich immernoch unter Null, muss doch aber über Null.
Was mach ich falsch ? ^^
zu c) um ehrlich zu sein hab ich mir noch keine Gedanken drüber gemacht, aber ich weiß ja die Punkte, da der Scheitel der Parabel die Fensterscheibe ja zufälligerweise schneidet.
Ergo hab ich meine Höhe, die Länge hab ich eh, Bong, habsch also nen Rechteck mit 1,75m Höhe und 1,5m Breite
edit: so, nach einer Pizza und zwei Bier habsch mein x1 einfach in die zweite Ableitung eingesetzt und Bingo

dann in die funktionsgleichung einsetzen und man bekommt ebenfalls 1 raus --> P(1|1)
für Aufgabe c habsch jetzt keinen Nerv mehr °_°
edit2:
so, hab c jetzt doch gemacht

hab einfach den Scheitelpunkt mit dr ersten Ableitung bestimmt.
f(x) = x² -3x +3
f'(x) = 2x -3 --> x = 3/2 --> Bingo, stimmt
einsetzen in f(x) --> 3/4 --> joap, stimmt auch ^^
und da der Scheitelpunkt die tiefste Punkt des Risses ist müssen wir ab da "abschneiden"
ergo ist das Teil am Ende noch stolze 1,50 auf 0,75 m groß

Last edited:
- Joined
- May 20, 2002
- Messages
- 24,877
- Reaction score
- 5
weil wir gerade im Mathefieber sind:
könnte mir jemand Schritt für Schritt erklären warum die Stammfunktion von f(x)= Wurzel aus x --> F(x) = 2x^2/3 / 3 ist ?
selbiges für f(x) = 1/x² --> F(x) = -1/x
steig da nich ganz hinter

edit: ich glaub ich komm doch dahinter, lasst mir noch ne halbe Stunde ^^
- Joined
- Oct 24, 2003
- Messages
- 11,481
- Reaction score
- 6
Erklär uns und dir zunächst mal, wie man eine Stammfunktion bilden kann 
zb. für f(x) = x oder f(x) = x^2
Dann sollte es offensichtlich sein.
Ansonsten überlege dir nochmal wie man f(x) = wurzel(x) als Exponent schreiben kann ( f(x) = x^?? )

zb. für f(x) = x oder f(x) = x^2
Dann sollte es offensichtlich sein.
Ansonsten überlege dir nochmal wie man f(x) = wurzel(x) als Exponent schreiben kann ( f(x) = x^?? )
- Joined
- May 20, 2002
- Messages
- 24,877
- Reaction score
- 5
f(x) = x --> F(x) = 1/2 x³ + c
f(x) = x² --> F(x) = 1/3 x³ + c
die n-te Wurzel aus x^m ist x^m/n
dann bekomm ich für f(x)=Wurzel aus x das hier raus: x^1/2
f(x) = x^n --> F(x) = 1/n+1 * x^n+1 + c
sek, ich rechne das mal kurz, maybe warsch nur zu doof

--->
F(x) = 1/(1/2 + 1) * x^(1/2 +1)
F(x) = 2/3 * x^3/2
joa... und nu ?
------ bei der zweiten krieg ich das hier raus O_o:
f(x) = 1/x² --> = x^-2
F(x) = -1/3 x^-3
Last edited:
- Joined
- Apr 8, 2007
- Messages
- 6,474
- Reaction score
- 0
kann mir wer die erste Ableitung von V = (1/3)*PI*s²-h²*h sagen PLZ ... also auf jeden Fall müsste das eine h wegfallen aber ich weiss nicht welchen Fehler ich noch habe....
ich soll von einem Kegel mit Seitenkante s=24cm das größte Volumen berechnen ...
als HB: hab ich aufgestellt V = (1/3)*PI*r^2*h
als NB : r²=s²-h²
das hab ich denn in einander eingesetzt :
V = (1/3)*PI*s²-h²*h
und jetzt müsste ich ja die erste Ableitung haben für den Maximalwert aber irgendwie hab ich ka was jetzt wegfällt genau
ich soll von einem Kegel mit Seitenkante s=24cm das größte Volumen berechnen ...
als HB: hab ich aufgestellt V = (1/3)*PI*r^2*h
als NB : r²=s²-h²
das hab ich denn in einander eingesetzt :
V = (1/3)*PI*s²-h²*h
und jetzt müsste ich ja die erste Ableitung haben für den Maximalwert aber irgendwie hab ich ka was jetzt wegfällt genau
Last edited:
- Joined
- Oct 24, 2003
- Messages
- 11,481
- Reaction score
- 6
kann mir wer die erste Ableitung von V = (1/3)*PI*s²-h²*h sagen PLZ ... also auf jeden Fall müsste das eine h wegfallen aber ich weiss nicht welchen Fehler ich noch habe....
Ich kenne jetzt zwar nicht die Definitionen und Mengen, welche hier angewandt werden sollen, aber ich gehe mal von diesem aus:
Code:
Berechnung der Ableitung - mal ganz elementar
V(x) = (1/3)*PI*s²-x²*x
/_\x V(x0 + /_\x) - V(x0)
---- = ---------------------
/_\y /_\x
(1/3)*PI*s²-(x0 + /_\x)²*(x0 + /_\x)-(1/3)*PI*s²-x0³
= ---------------------------------------------------- (Werte eingesetzt)
/_\x
-(x0 + /_\x)²*(x0 + /_\x)+x0³
= ----------------------------- (Werte zusammengefasst)
/_\x
-(x0²+2/_\x*x0+/_\x²)*(x0 + /_\x)+x0³
= ------------------------------------- (Quadrat ausgerechnet)
/_\x
-x0³-2/_\x*x0²-/_\x²*x0-/_\x*x0²-2/_\x²*x0-/_\x³+x0³
= ---------------------------------------------------- (Klammern aufgelöst)
/_\x
-3/_\x*x0²-3/_\x²*x0-/_\x³
= -------------------------- (Werte zusammengefasst)
/_\x
= -3x0²-3/_\x*x0-/_\x² (Durch das /_\x geteilt)
Nun müssen wir noch den Limes /_\x -> 0 bestimmen
V'(x0) = limes mit /_\x->0 für (-3x0²-3/_\x*x0-/_\x²) = -3x0²
Und das stimmt auch, denn ihr kennt ja sicher die Ableitungsregeln, wonach die Ableitung von f(x) = -x³ nämlich -3x² entspricht.
Legende:
/_\ := deltaSimilar threads
- Replies
- 33
- Views
- 8K
- Replies
- 5
- Views
- 22K