mal wieder mathe -.-

[Osbes]

War der Schnittpunkt nicht Teil der Aufagbe ?

 

[Mooff]

Käse.

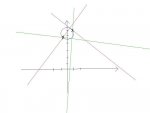
Das ganze kann man sogar Zeichnerisch widerlegen.

hrhr, genau das hab ich gestern kurz gemacht


hier mal zwei Geradenpaare:

 

[stefros]

War der Schnittpunkt nicht Teil der Aufagbe ?

selfpwnd

gj Mooff, das hab ich vorhin auch gemalt

 

[Osbes]

Und die sollten alle in dem blauen Kreis liegen (sofern ich ihn nicht per Hand eingezeichnet hätte)

selfpwnd

Gut, dann habe ich dies halt überlesen:P, aber mein Beweis ist trotzdem korrekt, das ist ja gerade das schöne an der Mathematik

 

[mope7]

btw, konnt nich pennen und hab jetzt meine Aufgabe gelöst

Fehler war bei der Info mit P

Da muss ich die zweite Ableitung nehmen, nicht die erste.

 

[blackplague]

btw, konnt nich pennen und hab jetzt meine Aufgabe gelöst

Fehler war bei der Info mit P

Da muss ich die zweite Ableitung nehmen, nicht die erste.

ich glaub das is nur noch nebensache bei denen

 

[mope7]

so, hab ma wieder was -.-

ich hab 4 Stangen die jeweils 2 Meter lang sind (die bilden dann die Steilkanten)
Diese soll ich zu einer Pyramide (Zelt ) mit quadratischer Grundfläche zusammenbauen.
Wie groß sind die Seitenlängen der quadratischen Grundfläche und die Höhe der Pyramide wenn ich ein möglichst großes Zeltvolumen haben möchte ?

Volumen ist: V = Grundfläche * h * 1/3

d.h.: V = a^2 * h * 1/3

Nebenbedingung (die mir so gesgat wurde O_o): 2^2 = (a^2 + d)/4

was mach ich denn jetzt ?

ich hab jetzt mit der Nebenbedingung (die ich jetzt auch schnalle --> a^2 + b^2 = c^2(c =2m) ) bisschen rumgespielt, da komm ich aber nur auf:

2^2 = (a^2 + h^2) / 4
16 = a^2 + h^2
4 = a + h
a = 4 - h
h = 4 - a

Oo

 

[huxl]

2² = h² + (d/2)² // pythagoras: katheten: halbe diagonale, quadratseite; hyothenuse: stange

(d/2)² + (d/2)² = 2(d/2)² = a² // pyrhagoras: katheten: 2mal die halbe diagonale; hypothenuse: seitenlänge
(d/2)² = a²/2

=>
2² = h² + a²/2
h² = 4 - a²/2
h = wurzel(4 - a²/2) = 2 - wurzel(a²/2) // die höhe in abhängigkeit der seitenlänge bei einer stangenlänge von 2

eingesetzt:
V = a² * (2-wurzel(a²/2) * 1/3

ableiteiten, maximum bestimmen, dann hast die seitenlänge des quadrats.


ach irgendwas is bei mir komisch
geh einfach mal davon aus, dass deine nebenebstimmung stimmt, lös sie nach h auf, setz das ganze in V = a² * h * 1/3 ein und bestimmt da das maximum

 

[mope7]

bor ich blick das nich

also nochma ob ichs gerafft hab:

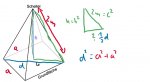
(siehe Bild)

aber ich kann d doch gar nit ausrechnen O_o
hab ja keine Angaben über a


edit: ich kann die Nebenbedingung nit nach h auflösen, weil in der Nebenbedinung gar kein ha vorkommt, nur d *g*

 

[stefros]

Es gibt eine Formel welche h abhängig von a und somit auch von d angibt (kA wozu man d braucht, das kannst m.E. auch weglassen).
Damit muss man eine dieser Variablen elimieren und dann das ganze in das Volumenintegral einsetzen.

Dann dieses ausrechnen und anschliessend das Maximum bestimmen (abhängig von a oder h).

viel Spaß

 

[mope7]

äh... wat ?

wie lautet denn diese Formel ? *flöt* ^^

 

[huxl]

das war nach meiner rechnung h = 2-wurzel(a²/2), wobei ich mir dessen nicht so sicher bin

 

[stefros]

Jo da brauchst du dieses Grüne Dreieck was du da rechts gemalt hast, da kriegst du h mit d/2 verbündet.
Dann kannst du in die Grundfläche noch ein Dreieck reinmalen in dem du d/2 mit a verbündet bekommst, dann noch d/2 elminieren und schwupps ist h mit a zusammen

Würde eher auf a(h) hinausgehen Huxl, über h lässt sich dann am Ende gut integrieren, zumindest anschaulicher als über a.

Weiss auch nicht ob deins stimmt, aber ich käme auf das:

a² = (s² - h²) / 2

wobei s = Stange = 2m ist.

 

[mope7]

ok, zum mitschreiben:

grünes Dreieck:

2² = (d/2)² + h²

Grundfläche mach ich nen Dreieck:

(d/2)² + (d/2)² = a²

ääääh also habsch: (d/2)² = a²/2

-->

2² = a²/2 + h² scheisse verflucht nochmal >_<

selbst wenn das richtig wäre würds mir doch null bringen weil ich immernoch zwei unbekannte hab O_o


och menno :/

gnatsch :/

 

[stefros]

jo richtig, danke Mope, mir is die ganze Pyramide nämlich beim integrieren grade voll divergiert weil ich 1/2 statt Faktor 2 hatte XD

a² = 2(s² - h²) ist richtig

baeh die Konstante ändert natürlich auch nix, doofes Teil

 

[mope7]

was ist denn nun wieder s² ? ^^ (edit: ach steht da oben ^^ hihi)

wo kommt das her ?

und wie mach ich dann weiter *heul*

wer hat sich nur sonen Mist ausgedacht

btw: ich hab grad erfahren, dass wir morgen nen Deutschtest über Werther schreiben

SUPER !

 

[stefros]

Jooo habs raus
s ist einfach ne Konstante, die eben vorgegbene.
In dem Fall 2 Meter, kann man aber ganz zum Schluss einsetzen.

Du musst dir jetzt überlegen wie du deine Pyramide aufbaust, du hast schon ne Formel für a², was ist denn a²? ^^

Achne ihr habt ja die ganze Volumenformel schon gegeben hab ich grad gehört, dann brauchst du nur noch den ganzen Knödel da einsetzen und aus V(a,h) ein V(h,s) wobei s=const. zu machen und dann dV/dh = 0 berechnen und schwupps fertig

 

[mope7]

ganz im Ernst, ich hab keine Ahnung....

ich blick da grad absolut nicht durch

für a² habsch deine Formel da oben - die setz ich ein in ?

a² is halt einer der Seiten von dem rechtwinkligen Dreieck unten: a² + a² = d²

ka... hilfe


könntest du nicht so liebesnwürdig sein die Rechenschritte hinzuschreiben, vielleicht kann ichs dann nachvollziehen Oo
ich hab echt ka was ich jetzt wo wie einsetzen muss damit ich was anderes rausbekomm

 

[stefros]

V(a,h) = a^2 * h * 1/3

da einsetzen das a² von oben

dann kommst zu V(h,s)

 

[James]

Nebenbedingung (die mir so gesgat wurde O_o): 2^2 = (a^2 + d)/4

äh, also somit wäre d = 1-a² was eigtl nicht sein kann oO