- Joined
- Sep 17, 2003
- Messages
- 3,693
- Reaction score
- 0
Hey,
in der Uni beschäftigen wir uns gerade mit der vollständigen Induktion. Vom Prinzip her ist mir klar wie das funktioniert, ich habe hier jedoch bei drei Aufgaben Probleme Umformungen nachzuvollziehen bzw. selbst umzuformen. Wäre nett wenn mir jmd weiterhelfen könnte.
1. Hier wurden nach einsetzen der IV Umformungsschritte durchgeführt, die ich nicht nachvollziehen kann, da scheinbar mehrere Schritte in einem gemacht wurden. Ich hätte die Umformung gerne mal in kleinen Schritten gesehen:
[n(n+1)]/2+n+1 = (n+1)(1/2 +1) = 1/2 *(n+1)(n+2)
2. Wenn ich folgende Umformung zurückrechne, komme ich zu dem Schluss, dass nachher etwas anderes rauskommt als vor der Umformung und ich vermute daher, dass hier ein Fehler vorliegen müsste. Überprüft das bitte mal und sagt mir ob die Umformung richtig oder falsch ist:
[n(n+1)]/2+n+1 = [n²+n+2n+2]/2 = [n²+3n+2]/2 = [(n+1)(n+2)]/2 "Bis hierhin klar, jetzt kommt der letzte Schritt, der in meinen Augen falsch ist": = [(n+1)(n+1)+1]/2
3. An dieser Stelle komme ich nach einsetzen der IV nicht weiter:
2-(n+2)/2^n + (n+1)/2^n+1
Die Form, die erreicht werden soll lautet: 2-[(n+1)+2]/2^n+1
Ich hoffe es findet sich jmd, der mir helfen kann.
Greetz
bAshTi
in der Uni beschäftigen wir uns gerade mit der vollständigen Induktion. Vom Prinzip her ist mir klar wie das funktioniert, ich habe hier jedoch bei drei Aufgaben Probleme Umformungen nachzuvollziehen bzw. selbst umzuformen. Wäre nett wenn mir jmd weiterhelfen könnte.
1. Hier wurden nach einsetzen der IV Umformungsschritte durchgeführt, die ich nicht nachvollziehen kann, da scheinbar mehrere Schritte in einem gemacht wurden. Ich hätte die Umformung gerne mal in kleinen Schritten gesehen:
[n(n+1)]/2+n+1 = (n+1)(1/2 +1) = 1/2 *(n+1)(n+2)
2. Wenn ich folgende Umformung zurückrechne, komme ich zu dem Schluss, dass nachher etwas anderes rauskommt als vor der Umformung und ich vermute daher, dass hier ein Fehler vorliegen müsste. Überprüft das bitte mal und sagt mir ob die Umformung richtig oder falsch ist:
[n(n+1)]/2+n+1 = [n²+n+2n+2]/2 = [n²+3n+2]/2 = [(n+1)(n+2)]/2 "Bis hierhin klar, jetzt kommt der letzte Schritt, der in meinen Augen falsch ist": = [(n+1)(n+1)+1]/2
3. An dieser Stelle komme ich nach einsetzen der IV nicht weiter:
2-(n+2)/2^n + (n+1)/2^n+1
Die Form, die erreicht werden soll lautet: 2-[(n+1)+2]/2^n+1
Ich hoffe es findet sich jmd, der mir helfen kann.

Greetz
bAshTi



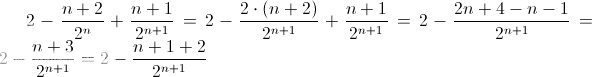
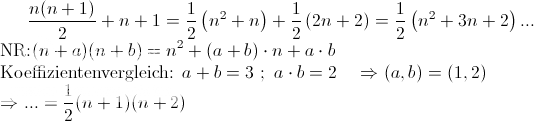
 mmd
mmd