Physikaufgabe

[Havoc]

Eigentlich keine Hausaufgabe, sondern nur eine Aufgabe, die wir als Übung für die Klausur rechnen wollten, aber auch nach ewigem Überlegen zu dritt einfach nicht gelöst bekommen.
Habt ihr da ne Ahnung? Ich weiß inzwischen schon garnichtmehr, was wir alles ausprobiert haben, kann das auch nichtmehr lesen, da mein armes Blatt durch das ganze Korrigieren zu sehr im Mitleidenschaft gezogen wurde

Aufgabe:
Ein Vollzylinder (Masse M=20kg, Radius R=15cm) wird von der Gewichtskraft einer zweiten Masse m=6kg, die über einen Faden und eine Rolle am Umfang des Vollzylinders angreift, auf horizontaler Ebene in geradlinige Rollbewegung versetzt.
Die Masse der Rolle und des Fadens sind zu vernachlässigen. Die Zusatzmasse Z zur Erfüllung der Rollbedingung braucht bei den Rechnungen keine Berücksichtigung zu finden.

Welche Schwerpunktgeschwindigkeit v[SUB]s[/SUB] erreicht der Vollzylinder, nachdem die Masse m um die Strecke h=2m herabgesunken ist?
Für das Trägheitsmoment des Vollzylinders bezüglich der Symmetrieachse längs des Vollzylinders gilt
J[SUB]s[/SUB]= 0,5M*r²

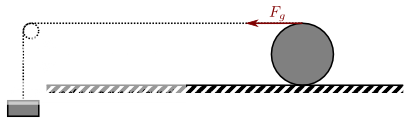
Ich weiß nicht, inwieweit man sich das ohne Bild vorstellen kann. Ich beschreib das sicherheitshalber mal:
Man sieht den Zylinder M, der auf einem Tisch mit der Schnur verbunden ist. Die ist dann auf einer Rolle gelagert, dessen anderes Ende mit m verbunden ist. m rauscht dann nach unten und der Zylinder bewegt sich in Richtung der Rolle.

Edit: Die Lösung wurde uns auch gegeben:

2,09m/s

 

[Golan]

Moh, ich hasse solche "sieht einfach aus aber das Ergebnis stimmt nicht" Aufgaben.

Also erst nochmal zum Problem, sieht das so aus?

Was ist eigentlich mit "Zusatzmasse Z zur Erfüllung der Rollbedingung" gemeint?

Mein Ansatz wäre folgender gewesen:
1. Das Drehmoment, das am Zylinder angreift, wird durch die Gewichtskraft verursacht und beschreibt die Winkelbeschleunigung α.
|M|=F·R=Jα mit F=mg
=>α = mgR/(0.5 MR²) = 2 mg/(MR)
2. Die Geschwindigkeit des Zylindermantels relativ zum Schwerpunkt hängt ab von der Winkelgeschwindigkeit.
v=R·∫α dt = 2 m/M g t
3. Der Schwerpunkt bewegt sich mit v relativ zum Boden, die obere Kante erneut mit v relativ zum Schwerpunkt. Die Länge des abgewickelten Seils (und damit die Fallhöhe) ist also:
s=2∫v dt=2 m/M g t²
4. Bei der Fallhöhe h=2m bedeutet das:
t₀=√(hM/(2mg)
v₀=2 m/M g t₀ = √(2 m/M g s)

Was leider etwa 3,5 m/s ist.

 

[Havoc]

Ne masse, die zwischen rollager und der Masse m hängt
und ja so siehts aus, nur spiegelverkehrt und bei M ist noch der Vektor der Gewichtskraft eingezeichnet. Also neben M